Equation of Wave

The symmetrical pulse created by a man on a string by moving his hand up and down, travels with speed $3 \mathrm{m} {\mathrm{s}}^{-1}$ on the string & his hands passes $6$ times in each second from the mean position.At $t=0$ the point in his hand moves downward.Then the point on the string at a distance $3 \mathrm{m}$ will reach its upper extreme first time at time $t=$

If $x-\alpha \sin \left(\omega t-\pi /6\right)$and $x=\alpha \cos \omega t$, then the phase difference between the two waves is 

The expression for a sinusoidal wave at a fixed location can be written as:

 In a region of constant potential

Equipotential surface of a greater distance from a collection of charge whose total sum is not zero one approximately.

A test charge is moved from lower potential point to a higher potential point. The potential energy of test charge will.

The transverse displacement at position $x$ and time $t$ in a string due to a travelling wave is given by $y(x, t)=$$3.0\cos (\pi x-4\pi t)\mathrm{cm}$, where $x$ is in centimeters and $t$ is in seconds. Which of the following statements is wrong?

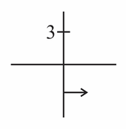
The equation of a wave travelling in a string can be written as $y=3 \cos \mathrm{\pi } \left(100t-x\right) \mathrm{cm}$. Its wavelength is 

A plane progressive wave is given by $y=2\cos 6.284(330t-x)$. What is the time period of the wave?

The relation between wavelength $\lambda$ and angular wavenumber $k$of the wave is 

The transverse displacement $y\left(x,t\right)$ of a wave on a string is given by $y\left(x,t\right)=e^{-\left(a{x}^2+b{t}^2+2\sqrt{ab}\mathrm{ x}t\right)}$. This represents a

Equation of a wave motion (with t in second and x in metre) is given by, $y=7 \sin \left(7\mathrm{\pi t}-0.04\mathrm{\pi x}+\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\right)$. The velocity of the wave is given by :

A wave of amplitude $A=0.2 \mathrm{m}$, velocity $v=360 {\mathrm{ms}}^{-1}$ and wavelength $60 \mathrm{m}$ is travelling along positive $x$-axis, then the correct expression for the wave is

The equation of a progressive wave is $y=8\sin \left[\pi \left(\frac{t}{10}-\frac{x}{4}\right)+\frac{\pi }{3}\right].$ The wavelength of the wave is,

The equation of a wave travelling on a string is $y=4\sin \left[\frac{\pi }{2}\left(8 \mathrm{t}-\frac{x}{8}\right)\right],$ where $x, y$ are in $\mathrm{cm}$ and $t$ in second. The velocity of the wave is

What is the relation between angular frequency and the time period of a wave?

Two graphs of the same harmonic wave are shown below. The graph $\left(1\right)$ on the left shows the displacement of wave $y$, as a function of position $x$ for a given instant of time. The graph $\left(2\right)$ on the right shows the displacement of the wave as a function of time $t$ for a given position. The speed of the wave is

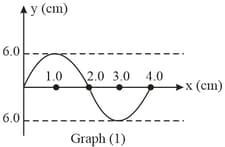
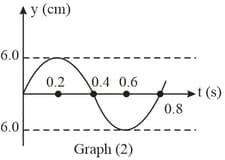
A harmonically moving transverse wave on a string has a maximum particle velocity and acceleration of 3 m/s and 90 m/s² respectively. Velocity of the wave is 20 m/s. Find the waveform.

The motion of particles of a wave at $x_1=0 \mathrm{cm}$ and $x_2=1 \mathrm{cm}$ are given by the following equations respectively. (displacement is in $\mathrm{cm}$)

$y_1=2\sin 3\mathrm{\pi }t$ and $y_2=2\sin (3\mathrm{\pi }t-\frac{\mathrm{\pi }}{8})$

Find the wave velocity.

In the above question, the displacement of particle at $t=1 \sec$ and $x=4 \mathrm{cm}$ is